Lab 13 Path Planning
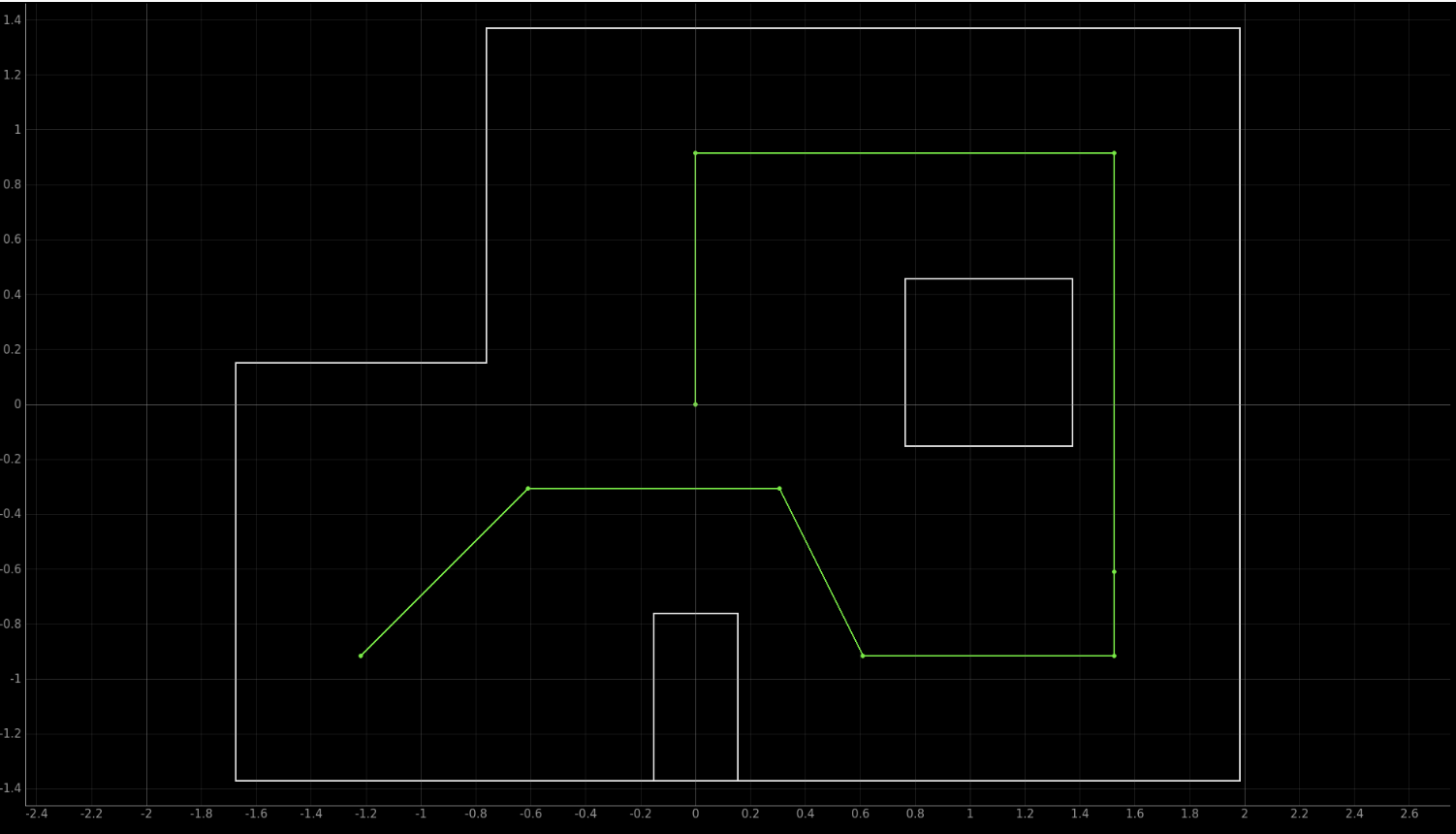
The final lab for this course gave us the opportunity to make use of every we had learnt in this course. The goal of this lab was to use the robot built in this course to navigate through a set of waypoints in the lab environment set up, as quickly and accurately as possible. This lab was very open ended and we were encouraged to try out different methods. The waypoints given below are the way points the robots needs to nagivate.
(-4,-3), (-2,-1), (1,-1), (2,-3), (5,-2), (5,3), (0,3), (0,0)
I collaborated with Krithik Ranjan (kr397) and Aparajito Saha (as2537). We worked together on this lab from start to end, including coding, implementation and testing. We worked on this lab during the last week of classes as well as the extra lab hours.
PID Control for Translation and Orientation
Regardless of which method the robot uses navigate the waypoints, we wanted to add functionality for the robot to (1) move an exact distance and (2) rotate for a certain angle. We wanted to use closed loop control to execute both these functionalities.
Orientation
We modified the orientation control code used in previous labs (lab 6,8,9,12) to turn the robot by a particular angle using PD control. The P gain was set to 1 and D gain was set to 0.5. When the TURN_ANGLE command is provided to the robot along with an angle as input via Bluetooth, the robot rotates clockwise by the provided input angle. The robot's orientation used in the localization module is using positive angles measured anticlockwise from the x axis. As we planned on using localization, for the sake of uniformity we created a mapping function to map the anticlockwise rotation angle to required robot input for the same result. As seen in previous labs, yaw angle measured using the IMU gyroscope was not accurate. The video below shows the robot's rotation for 360 degrees, which is clearly much more than the target. We used two-point calibration in the mapping function to fix this issue. We faced a lot of issues with orientation control as we had to tune the two point calibration every couple of minutes, as the battery was discharging fast due to heavy usage. The same calibration would not work for some angles, for example the robot would turn 90 degrees perfectly, but would not be able to accurately turn 270 degrees. Where possible (method 1), we tried to tune the target angles to ensure that the robot physically turned the required amount.
Translation
We wanted the robot to be able to move a certain distance, when provided with an input distance. We decided to use PID control on the ToF sensor readings from the sensor placed in the front to move the robot in a straight line for a certain distance. The robot uses the difference in the ToF sensor data at the start and current value to calculate the distance moved. We also take an average of 10 sensor readings in the beginning to ensure that the distance is accurate. We ended up using only PD control for translation with P gains set to 0.04 and D gain set to 0.1. The P gains was so low, because we the upper bound on the PWM duty cycle was 255. We had to change to P gain to 0.25 while moving very short distances. We added a bluetooth command called MOVE_FORWARD which takes in the distance (meters) to move and the PID gains as input and executes the translation motion. The controller also works with negative distances and moves the robot in reverse. We also added a safety mechanism, where the robot does not move ahead when where is an obstacle within 5 cm. The robot also does not move when the input distance to be travelled is more than the sensor reading at the starting point.
Onboard/Offboard Division
With the two PID controllers executed, we had a robot that could be driven from the Jupyter Notebook via Bluetooth. We had to make an important descision to make - which logic should be executed where. As there were multiple variables which had to constantly be retuned and we had minimal time while testing our runs in the lab setup, we decided to write the "global" logic on the Jupyter Notebook and the "local" logic on the Artemis. The orientation control, translation control and getting sensor data from a localization sweep was on the Artemis, rest of the logic was on the computer.
Method 1 - Open loop with PID control
To begin, we decided to implement a simpler version of the "rot-trans-rot" logic from lab 11 to move the robot through the wave points. The computer computer the actions required for the robot and sends them to the robot for execution using the orientation and translation PID controller. Given that our closed loop for orientation and translation worked well once tuned, we decided that this was a good starting point for us. We created functions to calculate the rotation 1 required to move from one position to other and the translation required to move from one position to other. The waypoints did not have any orientation associated with them, we just had to reach the waypoint's poisition. There was not use to calculate the second rotation angle, as the orientation at the target point did not matter. We created a loop that iterated through all the waypoints, with starting position as (-4,-3,45). In each iteration, it first calculated the required rotation and send the command to the robot, then did the same with translation. We had to add a delay for 1 second after sending the command to the robot to ensure that the movement was completed by the robot before sending the next command. Note that we chose to start the robot 45 degrees pose to skip a rotation in the first movement.
# Pseudocode for performing trajectory using PID
curr_pose = (-4, -3, 0)
trajectory = [(-4, -3),(-2, -1),(1, -1),(2, -3),(5, -3),(5, -2),(5, 3),(0, 3),(0, 0)]
ble.send_command(TUNE_PID)
for next_pose in trajectory[1:]:
# Calculate rotation required to get to next point and rotate
rot = calc_rot(curr_pose, next_pose)
ble.send_command(TURN_ANGLE)
# Calculate translation to get to next point and move
trans = calc_trans(curr_pose, next_pose)
ble.send_command(MOVE)
# Update pose
new_angle = normalize(curr_pose[2] + rot)
curr_pose = (next_pose, new_angle) To test our implementation, we started with a small portion of the trajectory and keep adding way points to it. While our approach may seem open loop, it is not entirely open loop as the computer calculates the distance it needs to move and the angle it needs to rotate. There is no feedback control implemented, so it is not closed loop either.
Using ToF sensor in front and back positions
For many paths in the trajectory, the ToF sensor needs to measure really long distances, especially from (-4,-3) and (5,-3). The sensor readings are quite noisy for such large distances. As the sensor readings are used for translation, this resulted in inaccurate forward movements or no movement at all due to faulty sensor readings. To overcome this issue, we decided to run the robot with the ToF sensor on the back and use negative distances. However, we still faced the issue at some points such as (1,-1). To overcome this, we decided to drive the robot backwards in some paths and forward in some. We added an additional component for each waypoint (-1/+1) sigifying where to drive the robot forward or in reverse. The robot starts with the ToF sensor in the back, if at any point we need to drive the robot forward, it does a 180 degree turn and positive translation distance is used. However, the stretch from (5,-3)/(5,-2) to (5,3) was still a long distance for the robot to move with the ToF sensor facing in one direction. To overcome this, we added a (5,0) way point, where the robot also switches its direction. This method really helped us achieve accurate translation distance.
The videos below show two of our best runs of using Method 1.
Using the 90 degree hack
The PID control worked quite well, but if it messed up at point, it meant that the all of the remaining trajectory might not be executed correctly. Most of our issues were due to orientation control, as the robot did not turn the exact angle when required to. After multiple runs, we realized that the region from (1,-1) -> (2,-3) -> (5,-3) was the most problematic. Reason being the 63 degree turn required at (1,-1) was never accurate. Usually the robot either overshot and collided with the bottom box or stopped before the target angle and later on while trying to move to (5,-3), collided with the right grid edge or missed the (5,-3) waypoint. This (1,-1) point also involved the ToF sensor position switch (180 turn), which added to the wrong orientation. To avoid this, we decided to tackle this region with the 90 degree hack. The robot first turned 90 degrees, then moved forward to point (1, -3), turned 90 degrees again and then moved to the (2,-3). While this took longer, we were much more accurate. We only used this hack for this region as the robot moved correctly in other location.
Analysis and Issues Faced
We faced many isseues with method, primarily because we had to retune a lot of the characteristics. We had to tune the orientation control as well as the two point calibration for the input angle every time before entering the grid. After a point, it got quite frustrating. The tuning for a 90 degree turn that works perfectly at one waypoint would not work at the other. For some time, we even wrote the indiviual movements as a sequence and tuned the robot for every single translation and rotation. This was not much use, as it meant we had to tune every movement repeatedly. The lack of feedback control meant that if the robot does not turn correctly at one point, it will never reach the next way point accurately. The error continues to accumulate. Sometimes this worked in our favor, for example if the robot rotated a little more at (2,-3) and would end up in (5,-4); the robot would rotate a little more at (5,-4) and correct itseld. We had a lot of runs where the robot would work perfectly up until the very end and mess up the turning at (0,3) and end up at (1,0) instead of (0,0). The video below shows one run, where by messing up the angle at point, the entire trajectory is not followed correctly.
Regardless of all the issues, when it worked it worked very well. We were targeting both speed and accuracy with this method. As our PID control worked with high speeds, the robot completed the trajectory very quickly. In our best run, the robot was on top of six of the way points, one cell away from one of the way points and half a cell away from another and completed the run in 26 seconds. We also have lots of partial runs, where the robot hits the waypoints in its trajectory accurately.
Method 2 - Localization
While the PID control worked reasonably well, we wanted to add a feedback control mechanism to the algorithm, so we decided to add localization. We could not run the prediction step and update step (as seen in lab 12 simulation), as there is no way to get the actual pose of the robot in the grid without user input. The actual pose of the robot is required for the prediction step to calculate the movement completed. There could have been a get around for this, by inputing the actual pose of the robot at every step and running the prediction step followed by the update step. We could have also used movement (rotation + translation) directly in the prediction step instead of providing the actual pose of the robot. However, we chose not to do so, due to the complexity of the implementation and lack of experience with the prediction step in a real environment. As seen in the second part of lab 12, we decided to run the update step and get the estimate of the robot's position based on the belief probabilities. We had to re-initialize the grif beliefs before every update step, as we are only running that. Running the update step, does a full observation sweep of the surrounding, collecting ToF sensor data at 20 degree increments going anticlockwise. Then it updates the belief probablity for each pose, we assume that the pose with the highest probability is the position of the robot.
Localization at one waypoint
We started off by adding localization only at one waypoint (2,-3). Until this point, the robot moves as seen in Method 1 and localizes after completing the movement to (2,-3). The robot uses the position estimate to calculate its movement to the next waypoint (5,-3). We also added an extra rotation after the translation for the robot to stop at (5,-3) with 0 degree orientation. As this is how the robot would have reached the waypoint if it had actually travelled from (2,-3). We chose to localize at this waypoint because the robot always has problems in reaching this way point correctly. We soon realized that the robot reaches the vicinity of (5,-3) waypoint but at a different orientation instead of the required 0 degrees. The rest of the trajectory was not being completed properly. This might be cause of the discretization of the orientation in the localization module, discussed in lab 12.
Complete Localization
We decided to overcome this issue by locallizing at every waypoint. We modified the loop from method one to localize at the end of every movement. Then use the position estimate as the current position of the robot, while calculating the movement to the next waypoint in the next iteration. The video below shows localization with a simple algorithm.
# Pseudocode for performing trajectory with localization and point checking
trajectory = [(-4, -3),(-2, -1),(1, -1),(2, -3),(5, -3),(5, -2),(5, 3),(0, 3),(0, 0)]
curr_pose = (-4, -3, 0)
next_pose = (-2, -1)
done = False
i = 1
ble.send_command(TUNE_PID)
while not done:
# Check if near the next point
if (calc_trans(curr_pose, next_pose) < 0.35):
i = i + 1
next_pose = trajectory[i]
if i == len(trajectory) - 1:
done = True
# Calculate rotation required to get to next point and rotate
rot = calc_rot(curr_pose, next_pose)
ble.send_command(TURN_ANGLE)
# Calculate translation to get to next point and move
trans = calc_trans(curr_pose, next_pose)
ble.send_command(MOVE)
# Localize
loc.get_observation_data()
loc.update_step()
# Update pose from belief
curr_pose = loc.belief
# Reinitialize grid belief as only update step
loc.init_grid_beliefs()Deciding the next target
In the video above, you can see that the robot does not realize when it misses a way point and moves on to the next one. If the robots misses a way point, in the next loop iteration it tries to move to the next way point. We fixed are algorithm such that if after localizing the robot realizes that its current estimated position is not the way point it was trying to move to, in the next iteration it continues to move to that way point. Only if the estimated position is equal to the waypoint it was trying to hit, does it move to the next way point. The video below demonstrates a part of the trajectory with this algorithm.
Setting error margins
In the video above, the robot repeatedly tries to hit a single way point (-2,-1). Due to weak localization estimate (discretization to grid cell centers only) and overshooting while executing a very small translation movement, even through the robot passes over the waypoint multiple times, it never actually stops there so it does not consider that it has hit the way point. Instead the robot keeps oscillating among the grid cells adjacent to the way point. We realized that we were being too strict with the robot and needed to add some error margin. We added an error margin of 35 cm, if the robot is within 35 cm of the way point, it considers to have hit it and moves on to the next one. This small error margin will include the top, bottom, left and right grid cells but not the diagonally adjacent ones. The videos below shows the robot executing with this method. Another possible method of overcoming this issue would have been to calculate if the robot has crossed the waypoint in during the movement, but checking if the movement from previous position to current estimate passes through the waypoint. However, the localization estimates are often wrong so we did not execute this method.
# Pseudocode for performing trajectory with localization and point checking
trajectory = [(-4, -3),(-2, -1),(1, -1),(2, -3),(5, -3),(5, -2),(5, 3),(0, 3),(0, 0)]
curr_pose = (-4, -3, 0)
next_pose = (-2, -1)
done = False
i = 1
ble.send_command(TUNE_PID)
while not done:
# Check if near the next point
if (calc_trans(curr_pose, next_pose) < 0.35):
i = i + 1
next_pose = trajectory[i]
if i == len(trajectory) - 1:
done = True
# Calculate rotation required to get to next point and rotate
rot = calc_rot(curr_pose, next_pose)
ble.send_command(TURN_ANGLE)
# Calculate translation to get to next point and move
trans = calc_trans(curr_pose, next_pose)
ble.send_command(MOVE)
# Localize
loc.get_observation_data()
loc.update_step()
# Update pose from belief
curr_pose = loc.belief
# Reinitialize grid belief as only update step
loc.init_grid_beliefs()Robot gets stuck in the corner
During our test runs, we noticed that the localization works quite well for the first half of the trajectory, but the robot keeps getting stuck after reaching the (5,-3)/(5,-2) way point. In this corner, the robot can only move forward to the other side of the box through a narrow 2ft wide region. Many times, the robot tries is at a negative angular orientation around the point (5,-3) and needs to do turn an obtuse angle to face towards the next way point (5,3). During these large rotations, the robot usually overshoots and faces the obstacle. The rotation calculation might also be inaccurate due to dicretization of the angles in the localization module. For example, if the robot is at a -0.5 degree angular position, the localization modules discretizes this as -10 degrees. This means the robot will turn 100 degrees instead of the actual 90.5 degrees it needed to turn. The robot now faces the obstacles and wants to move forward for 6 ft. The safety guard mechanism will not allow the robot to move ahead. The robot will localize again, even it localizes correctly it will try to move towards (5,3) through the obstacle, as it does not account for the obstacle. The robot gets stuck and repeatedly localizes in the same area.
We changed the saftey mechanism to allow the robot to move as far as 10 cm from the obstacle. However, this resulted in the robot going even closer to the box and not being able to get out of there. A possible mechanism could have been to rotate the robot 180 degrees, move back and then retry hitting the waypoint. Or we could have moved the robot to an area outside the corner if it had been stuck in that region for more than 4 times. Due to lack of time we were not able to implement these algorithms.
Method 3 - Localization completing the waypoints in reverse order
We kept facing the same issue of getting stuck behind the box while running localization and executing the trajectory as given. We noticed that the robot only had to make 90 degree angles for the second half of the trajectory, which the robot executes very easily so there is less room for error. We decided to complete the trajectory in reverse order with the existing localization algorithm. This method worked and we got some decent runs where the robot was able to hit most of the waypoints. Because of the 1ft error margin, it did consider the adjacent blocks as hitting the waypoint, we hope this is acceptable.
I was quite impressed with the robustness and self-correcting property of the localization algorithm. In the second video shown above, the robot first localizes incorrectly at position (0,3), thinking it is at position (6,2). So it moves in the wrong direction, but then it localizes correctly and moves back to the way point. Please find the localization output for the run attached in the appendix. While the localization method is much slower than Method 1, it is more robust and self reliant. We had an average run time of 4 mins on our localization runs. The most of the time taken was due to the observation sweep, sending the data over bluetooth, initializing the grid cells estimating the position.
Conclusion
I felt that this was the best out of all the labs because I got the opportunity and time (mostly, should have started earlier but I had exams and other projects) to implement every thing that I had learnt in this course. It was amazing to see the robot implement the trajectory "autonomously" using localization. Towards the end, we were so into the project, we kept trying to come up with better solutions or trying it again for one more run. I wish we had not spent so much time tuning the PID for method 1 and tried out other path planning solutions. I also loved the atmosphere in the lab during the extra lab days. Everyone was working together, we were cheering for each others robot; I could not think of a better project to work during the last week of my undergrad.
I enjoyed this course a lot and would rank it one of the top courses I have taken at course. It was the perfect overview of Robotics; it included everything soldering the components to controlling the robot car as well as high level localization algorithms. Most importantly this course taught me how to deal with problems that occur with robots in the real world. While it was quite time consuming, I would still say it was worth it. As one of the few CS majors in this course, I would definetly recommend it to anyone interested in Robotics. I love the openended and collaborative nature of this course. A huge thank you to the amazing Professor Petersen, Vivek, Jonathan, Jade, and the rest course staff for being so amazing through out the semester and helping us with everything.
Appendix
A1 - Output for localization run.
2022-05-20 02:23:30,354 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:23:30,357 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:23:30,786 | INFO |: Movement: 1
2022-05-20 02:23:30,787 | INFO |: Currently At : (0.0, 0.0)
2022-05-20 02:23:30,787 | INFO |: Going to : (0.0, 3.0)
2022-05-20 02:23:30,904 | INFO |: Localizing
2022-05-20 02:23:56,169 | INFO |: Update Step
2022-05-20 02:23:56,185 | INFO |: | Update Time: 0.013 secs
2022-05-20 02:23:56,193 | INFO |: Belief: (1.0000000000000009, -3.0, -170.0)
2022-05-20 02:23:56,200 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:23:56,206 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:23:56,209 | INFO |: Movement: 2
2022-05-20 02:23:56,210 | INFO |: Currently At : (1.0, -3.0)
2022-05-20 02:23:56,218 | INFO |: Going to : (0.0, 3.0)
2022-05-20 02:23:56,881 | INFO |: Localizing
2022-05-20 02:24:21,773 | INFO |: Update Step
2022-05-20 02:24:21,797 | INFO |: | Update Time: 0.008 secs
2022-05-20 02:24:21,797 | INFO |: Belief: (6.0, 2.0, -30.0)
2022-05-20 02:24:21,806 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:24:21,807 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:24:21,811 | INFO |: Movement: 2
2022-05-20 02:24:21,812 | INFO |: Currently At : (6.0, 2.0)
2022-05-20 02:24:21,812 | INFO |: Going to : (0.0, 3.0)
2022-05-20 02:24:22,624 | INFO |: Localizing
2022-05-20 02:24:48,185 | INFO |: Update Step
2022-05-20 02:24:48,196 | INFO |: | Update Time: 0.010 secs
2022-05-20 02:24:48,199 | INFO |: Belief: (0.0, 2.0, -170.0)
2022-05-20 02:24:48,203 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:24:48,205 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:24:48,207 | INFO |: Movement: 3
2022-05-20 02:24:48,210 | INFO |: Currently At : (0.0, 2.0)
2022-05-20 02:24:48,213 | INFO |: Going to : (5.0, 3.0)
2022-05-20 02:24:49,024 | INFO |: Localizing
2022-05-20 02:25:13,858 | INFO |: Update Step
2022-05-20 02:25:13,874 | INFO |: | Update Time: 0.017 secs
2022-05-20 02:25:13,878 | INFO |: Belief: (5.000000000000001, 2.000000000000001, 10.0)
2022-05-20 02:25:13,882 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:25:13,884 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:25:13,887 | INFO |: Movement: 4
2022-05-20 02:25:13,890 | INFO |: Currently At : (5.0, 2.0)
2022-05-20 02:25:13,893 | INFO |: Going to : (5.0, -2.0)
2022-05-20 02:25:14,577 | INFO |: Localizing
2022-05-20 02:25:39,189 | INFO |: Update Step
2022-05-20 02:25:39,200 | INFO |: | Update Time: 0.010 secs
2022-05-20 02:25:39,203 | INFO |: Belief: (5.0, -1.0, -90.0)
2022-05-20 02:25:39,207 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:25:39,207 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:25:39,212 | INFO |: Movement: 5
2022-05-20 02:25:39,214 | INFO |: Currently At : (5.0, -1.0)
2022-05-20 02:25:39,217 | INFO |: Going to : (5.0, -3.0)
2022-05-20 02:25:39,547 | INFO |: Localizing
2022-05-20 02:26:04,379 | INFO |: Update Step
2022-05-20 02:26:04,395 | INFO |: | Update Time: 0.016 secs
2022-05-20 02:26:04,396 | INFO |: Belief: (6.000000000000001, -3.999999999999999, -90.0)
2022-05-20 02:26:04,398 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:26:04,399 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:26:04,400 | INFO |: Movement: 5
2022-05-20 02:26:04,400 | INFO |: Currently At : (6.0, -4.0)
2022-05-20 02:26:04,402 | INFO |: Going to : (5.0, -3.0)
2022-05-20 02:26:05,162 | INFO |: Localizing
2022-05-20 02:26:29,345 | INFO |: Update Step
2022-05-20 02:26:29,355 | INFO |: | Update Time: 0.010 secs
2022-05-20 02:26:29,361 | INFO |: Belief: (4.0, -2.0, 150.0)
2022-05-20 02:26:29,364 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:26:29,364 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:26:29,370 | INFO |: Movement: 5
2022-05-20 02:26:29,371 | INFO |: Currently At : (4.0, -2.0)
2022-05-20 02:26:29,375 | INFO |: Going to : (5.0, -3.0)
2022-05-20 02:26:30,244 | INFO |: Localizing
2022-05-20 02:26:55,144 | INFO |: Update Step
2022-05-20 02:26:55,154 | INFO |: | Update Time: 0.010 secs
2022-05-20 02:26:55,162 | INFO |: Belief: (5.0, -3.0, -30.0)
2022-05-20 02:26:55,165 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:26:55,166 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:26:55,171 | INFO |: Movement: 6
2022-05-20 02:26:55,172 | INFO |: Currently At : (5.0, -3.0)
2022-05-20 02:26:55,177 | INFO |: Going to : (2.0, -3.0)
2022-05-20 02:26:55,972 | INFO |: Localizing
2022-05-20 02:27:20,460 | INFO |: Update Step
2022-05-20 02:27:20,475 | INFO |: | Update Time: 0.015 secs
2022-05-20 02:27:20,475 | INFO |: Belief: (3.0, -3.0, -170.0)
2022-05-20 02:27:20,482 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:27:20,486 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:27:20,488 | INFO |: Movement: 7
2022-05-20 02:27:20,488 | INFO |: Currently At : (3.0, -3.0)
2022-05-20 02:27:20,493 | INFO |: Going to : (1.0, -1.0)
2022-05-20 02:27:21,126 | INFO |: Localizing
2022-05-20 02:27:45,180 | INFO |: Update Step
2022-05-20 02:27:45,199 | INFO |: | Update Time: 0.020 secs
2022-05-20 02:27:45,209 | INFO |: Belief: (1.0, -1.0, 110.0)
2022-05-20 02:27:45,213 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:27:45,215 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:27:45,217 | INFO |: Movement: 8
2022-05-20 02:27:45,220 | INFO |: Currently At : (1.0, -1.0)
2022-05-20 02:27:45,222 | INFO |: Going to : (-2.0, -1.0)
2022-05-20 02:27:46,257 | INFO |: Localizing
2022-05-20 02:28:10,868 | INFO |: Update Step
2022-05-20 02:28:10,876 | INFO |: | Update Time: 0.008 secs
2022-05-20 02:28:10,883 | INFO |: Belief: (-2.0, -1.0, 150.0)
2022-05-20 02:28:10,887 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:28:10,888 | INFO |: Uniform Belief with each cell value: 0.00051440329218107
2022-05-20 02:28:10,892 | INFO |: Movement: 9
2022-05-20 02:28:10,893 | INFO |: Currently At : (-2.0, -1.0)
2022-05-20 02:28:10,897 | INFO |: Going to : (-4.0, -3.0)
2022-05-20 02:28:11,936 | INFO |: Localizing
2022-05-20 02:28:36,906 | INFO |: Update Step
2022-05-20 02:28:36,924 | INFO |: | Update Time: 0.018 secs
2022-05-20 02:28:36,930 | INFO |: Belief: (-3.0, -2.0, -110.0)
2022-05-20 02:28:36,932 | INFO |: Initializing beliefs with a Uniform Distribution
2022-05-20 02:28:36,933 | INFO |: Uniform Belief with each cell value: 0.0005144032921810
2022-05-20 02:28:37,502 | INFO |: Done