Go To:
Home Page
Milestone 4

Milestone 3: Maze Exploration Algorithm

Goals:

In simulation and in real life, we must:

In simulation:

Team members:

Materials Used:

We decided that the Depth First Search(DFS) is the most appropriate algorithm to start with. Here is our logic behind our decision:

// Depth First Search - Basic Structure
public class dfs {
    Stack s= (u);                      // The list of grids that have to be visited
    while (s is not empty) {           // If the stack is empty, the robot is done!
        u= s.pop();                    // Next target grid is the topmost grid on stack
        if (u is not visited)          
            visit u;
        for (Neighbors of u) {         // Add the neighbor grids of the current location to the stack.
            s.push(u);
        }
    }
    return;
}

Some of initializations and definitions should be clarified:

  1. Grid
/** 5 by 4 array is initialized. (row, column) is reversed to represent
* (x,y). (Ex. (row 2, column 3) -> (x,y) = (3,2). X,Y coordinate origin is
* at the top left. The robot's starting position is (x,y) = (3,4) */
public void gridInit() {
	grid= new Node[5][4];
	for(int i= 0; i < 5; i++) {
		for (int j= 0; j < 4; j++) {
			grid[i][j]= new Node(null, false, false, j, i);
		}
	}
}

 2. Wall

/** User-input maze. Decimal representative of wall location on each grid by
	 * 4bit binary number (msb)'(W)(E)(S)(N)'(lsb) */
public int[][] mazeInput1= new int[][] {
	{9,1,3,5},
	{8,6,13,12},
	{12,11,6,12},
	{8,3,7,14},
	{10,3,3,7}
};
  1. Node: In the Arduino language, we will implement unsigned 16 bit integer for each array element. In our simulation on Java, we created a Node object that contains the following information. *isSpecial indicates a node which we do more calculations on than non-special nodes. It is used later for backtracking algorithm.
/** Each grid contains the following information */
public class Node {
	private Node bckPntr;
	private boolean visited;
	private boolean isSpecial;
	public int x;
	public int y;
}

The key points of the algorithm are as followed:

/** Check the neighbors of the grid, except for the grid from which the robot comes from.
 * (Direction tells us where the robot is coming from. The grid that the robot
 * is facing is checked first */
private List<Node> getPath(Node current) {
	List<Node> paths= new LinkedList<Node>();
	int directx= current.x - current.bckPntr.x;  // If it is 1, the robot is heading West
	int directy= current.y - current.bckPntr.y;  // If it is 1, the robot is heading South
	if (directx == 1) {  // Faces East
		if (maze[current.y][current.x].charAt(1) == '0') paths.add(grid[current.y][Math.min(3, current.x + 1)]);
		if (maze[current.y][current.x].charAt(3) == '0') paths.add(0, grid[Math.max(0, current.y - 1)][current.x]);
		if (maze[current.y][current.x].charAt(2) == '0') paths.add(0, grid[Math.min(4, current.y + 1)][current.x]);
	}
	
	/*.......... Cases for facing West, North, and South.................*/
	return paths;
}

/** Backtracking using Backpointers */
while (!isPathOpen(position, u)) {
    prev= position;
	position= position.bckPntr;
	path.add(position);
}
//The robot is finally at the adjacent grid of the target grid!
u.bckPntr= position;
position= u;

This is the part where we can find the most apparent inefficiency of DFS. DFS cannot intelligently find its way to a remote target grid, because all the information it stores is the backpointer of each grid (this is unfortunately why DFS is very memory efficient!).

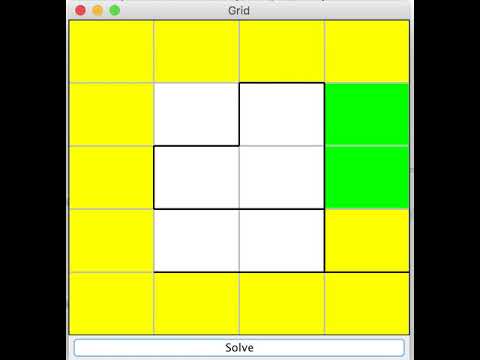
Here’s an example of maze that demonstrates this inefficiency in backtracking. If we use a regular backpointer method for backtracking, the robot chooses a non-ideal path to get to the remote target grid.

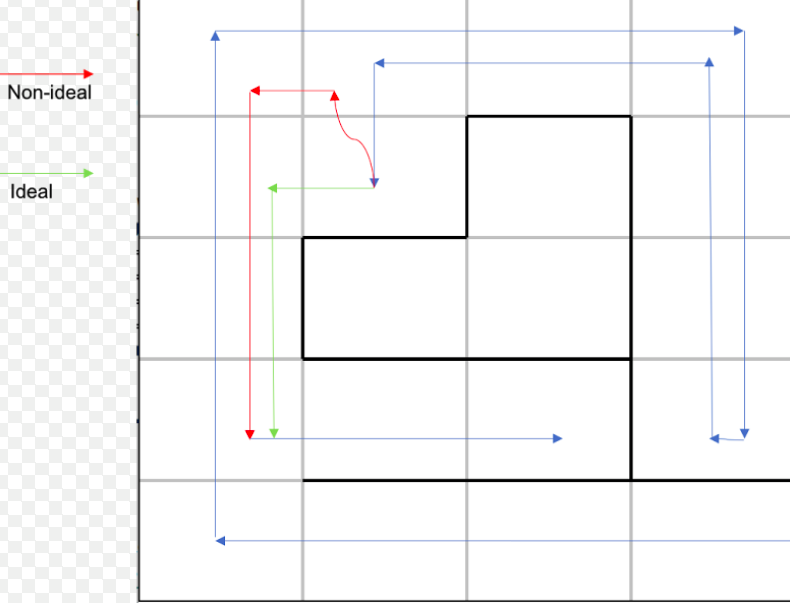
PICTURE #1

We tried to improve DFS’ regular backtracking method by calculating the Manhattan distance between each neighboring grid and the target grid whenever necessary (a grid whose isSpecial value is true!), and choose the one that has the shortest distance, instead of relying on the backpointers.

for (Node n: neighbors) {
    int distance= (Math.abs(n.x-u.x)) + (Math.abs(n.y-u.y));
    if (distance < temps && n != prev && n.visited) {
	    position.bckPntr= n;
		temps= distance;
	}
}

Here’s a video clip of GUI demonstrating the algorithm’s improved efficiency in backtracking. We marked the once-visited grid with yellow and twice-visited grid with green (third-visited grid with blue). Walls are marked with black and boundaries of grids without wall with light gray.

Video 1

Random Maze Generator

Upon the successful completion of simulation on several mazes, our team was inclined to prematurely conclude that the work on algorithm was done. However, we wanted to test the efficiency and robustness further, in particular with the ‘corner’ cases, in which the mazes are intentionally designed to confuse the robots. So far, due to our inexperience with the testing with physical mazes, we were not ready to artificially come up with good sets of corner cases. In other words, we had to generate as many random mazes as possible and try our algorithm on.

It is easy to draw 5 by 4 arrays on paper. On the contrary, it is very slow and toilsome to convert the walls into binary numbers and hard-type them onto the program. Therefore, we wrote a simple script that randomly generates mazes. We assign the ‘level’ parameter from 0 to 1 that is proportional to the number of walls.

Arduino Language

 The next step is to transfer our codes in Java to Arduino. Our codes in simulation were not directly transferrable to Arduino, and we had to write a new program, albeit with the same logic process. Please refer to our code file on Github repository for details. Several things to point out:

PICTURE #2

Before we end the section on algorithm, we want to show you one more video of GUI simulation. The unreachable areas (the areas that are completely surrounded by walls) are marked with gray color (then you know the robot finished its exploration!)

Video 1

In real life:

In order to test our algorithm in real life, we had to create a FSM to control the movements of our robot, shown below:


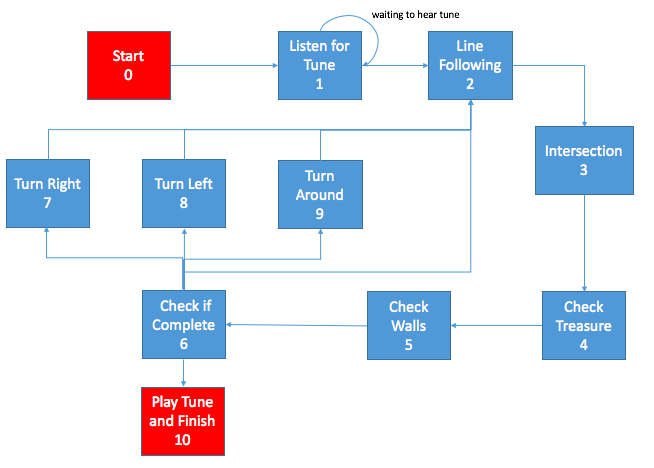
In the competition, the robot will start at State zero, the “start state”, and automatically enter to State One, in which the robot will be waiting for the tone. These two states however are currently bypassed in this Milestone.

For the Milestone, the robot will automatically start in State Two (line following), the robot will start line following immediately after starting. However, in the final, we will start the robot in the intersection state to check for walls immediately after initiating.

State four (check treasure) and state five (check walls) are pretty straightforward. For this Milestone, we did not implement any treasure detection, however, wall detection is implemented to determine what the next block the robot should traverse to. For wall detection, we used the wall detection code written in Milestone 2.

State 6 (Check if Complete) is the state where we will be implementing the search algorithm and determine whether the entire maze has been searched. If more exploration is needed, the search algorithm will determine if the robot needs to turn right, left, or turn around;. This is why this state has five options for the next state.

Once the robot has the correct orientation, provided that the maze has not yet been fully explored, the robot will go back and enter the line following state (state 2) again, starting the entire loop again.

Here is one of the robot’s attempts at travelling through the maze:

Video 1

If you have just watched the video, you might be shocked at how bad our robot looks and how its behavior does not seem to make any sense. But in fact, it does not look as bad as it seems.

Firstly, as you will read soon, we are in the process of making a complete overhaul of our original robot design. Because we have been focusing on the redesigning and reshaping parts, our robot has been neglected. The sensor connections are pretty weak and inconsistent with all the lines and connectors flying around each other; the wall sensors are duct-taped and tilted in unpredictable direction, which makes it very hard to set any reasonable wall-threshold value. But again, we plan to redevelope the entire robot this coming week with new chassis and new line sensors. Please bear with us until our robot is reborn with a complete transformation.

But, algorithm-wise, we see some progress. The robot is initialized to start at the bottom-right corner, so it assumes there are walls on its east side. We put it on a very tiny maze, where the north side is blocked with a wall. After seeing the north wall, it makes 180 degree turn and comes back to its original position. Again, the robot’s west side looks empty, but in robot’s perspective, it is always blocked, because is still at the last column, which is covered with walls by default. It does not have anywhere to go, and it finishes the exploration and give us its finish sign with red LEDs.

Earlier before this physical testing, we ran the robot while holding it with our hands and printing out the current location the robot is supposedly going using print statement in serial monitor. We verified that when we do not block the wall sensor, it goes through the grid # 19, 15, 11, 7, 3, and then 2, 1, 0 and so on, at least on the serial monitor, as it should (going up north until it hits the topmost row, where it sees this imaginary wall by our default setting, and turning left and go straight again). We also verified that when we block its sensor by putting a block of wall next to it (while we simulate the intersection point by blocking the line sensor), it turns to 14 from 15. And this video seems to complement our earlier testing to a certain extent. Of course, there’s a long way to go, because backtracking–finding a remote node–uses a different logic process within the code.

Roadblocks

Our largest roadblock for the real life test of our algorithm was the fact that our robot was still missing a lot of features, the most important being wall sensing. We are in the process of redesigning our robot (look at the improvements section for details), but we realized we wouldn’t have time to test the algorithm with the new designed robot before the due date, so we decided to use our original robot.

Improvements for the Future:

In terms of our algorithm, we still need to consider the following:

Right now, we also have a lot of modifications we want to make to our robot, including the following:

  1. Changing the structural design of our robot
    • Laser cutting a new chassis
    • Placing the motors on top of the chassis.
    • 3D printing a new ball bearing holder to match the size of our changes
  2. Printing a PCB
  3. Implementing a new line sensor

1. New Structural Design:

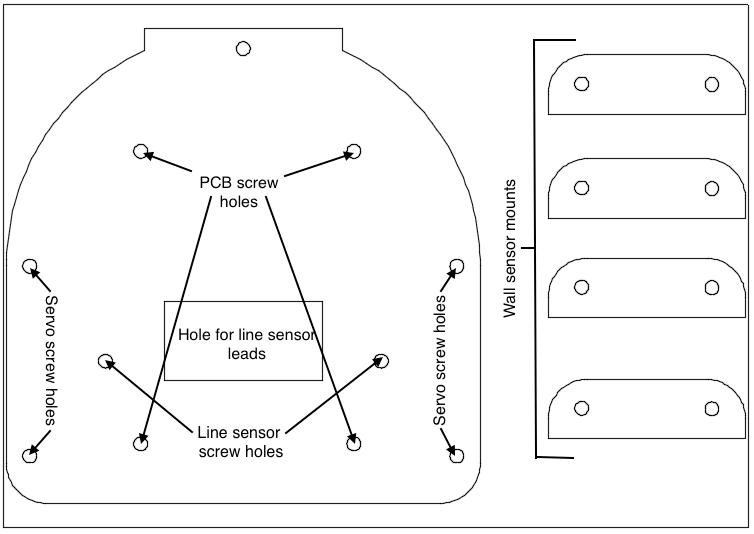
The overall purpose of the new chassis is to make room for the new line sensor and PCB. The wall sensor mounts will also be laser cut and glued directly onto the chassis.

2. Schematic of new PCB:

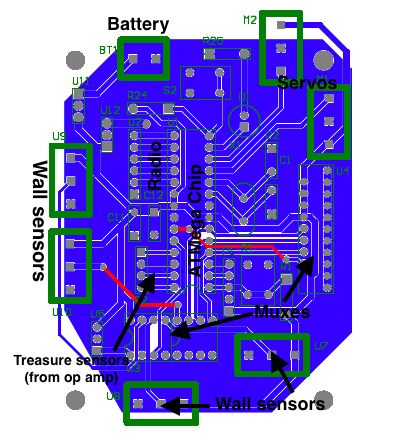
INSERT PCB DIAGRAM

This diagram gives you a general idea of how our PCB will work. Once we mill out our design and test it, we will see what changes need to be made. We might also add an op amp circuit on a separate PCB for our microphone, but that isn’t included in the diagram right now.

3. New Line Sensor:

The new line sensor we chose is the Pololu QTR-8A Reflectance Sensor Array. A picture of our sensor can be seen in Figure 1. This line sensor has the following specifications:

In order to be able to use all 8 of the line sensors, we had to add a mux to it as seen in Figure 2. We soldered the pins of the line sensor to the corresponding pins of the mux. In hindsight this wasn’t the best idea since it eliminated some of our flexibility in how we use the line sensor.

Go To:
Home Page
Milestone 4