Report
This study focuses on buzzer-beater shots in the NBA, which are shots taken in the final seconds of a game with the goal of scoring before the game clock runs out.
Often when buzzer beater shots are taken, fans watching from the stadium or at home, are on the edge of their seats and holding their breath. It feels like time slows down as we all wait for the shot to reach the basket. If the deciding shot makes its way into the basket, the entire stadium erupts in cheers and excitement.
In addition to being socially significant, these shots can also be game deciding. These shots are the most important in the game as, when attempted, they are the difference between a win and a loss. Thus, analyzing the stats behind successful buzzer-beater shots is important to gain insight into what possible strategies coaches can employ to make hitting one more likely.
Using a dataset containing an entry for almost every successful game winning buzzer-beater shot in NBA history, this project attempts to discern which factors play a role in the success of such shots. Analyses performed include a player’s performance vs. the number of these shots that they have made, the distance a player is from the basket vs. the year the shot was made, and the likelihood of a player making a shot based on their performance in the game and whether or not the shot was assisted. While the results of the first and second of these analyses were found to be insignificant, the third yielded significant results, indicating that game performance and whether or not the shot was assisted are significant indicators of the success rate of these shots, particularly the latter of these two variables. We ultimately conclude that the probability of whether or not a player who attempts a buzzer-beater shot will make it in the basket likely comes down to non-quantifiable measurements and is thus very difficult to measure.
Motivation
Why was this dataset created?
Who funded the creation of the dataset and who created it?
Composition
What are the observations (rows) and the attributes (columns)?
How many observations are in the dataset
Is the data a sample of a larger population?
Are there null values in the dataset?
Collection process
How was the data collected and where was it collected from?
If people are involved, were they aware of the data collection and if so, what purpose did they expect the data to be used for?
What processes might have influenced what data was observed and recorded and what was not?
Pre-processing/cleaning/labeling
What preprocessing was done, and how did the data come to be in the form that you are using?
How will missing values be handled?
Was the raw data saved and how can it be found?
Uses
What other tasks could the dataset be used for?
Is there anything about the dataset that future users should know?
What should the data not be used for?
Game Score vs. Number of Game Winning Buzzer-Beater Shots made:
# A tibble: 1 × 1
mean_shots_made
<dbl>
1 1.52
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 1.13 0.120 9.39 4.00e-19
2 mean_game_score 0.0258 0.00718 3.59 3.70e- 4Estimated Linear Model:
\[ \widehat{Shots~Hit} = 1.129 + 0.026 \times mean~game~score \]
Interpretation of Slope: For every 1 point increase in a player’s mean game score across every game they have made a game winning buzzer-beat shot, the number of game winning buzzer-beater shots they make increases by 0.026 shots, on average.
Interpretation of intercept: When mean game score is 0, the number of buzzer-beater shots made is 1.129, on average.
The mean number of game winning buzzer-beater shots made by players who have made at least one such shot is ~1.52 shots.
Year vs. Average Distance from Basket of Buzzer-Beater Shot:
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -10.2 74.7 -0.136 0.892
2 year 0.0134 0.0376 0.356 0.723\[ \widehat{average~distance} = -10.16 + 0.0134 \times year \]
Interpretation of Slope: For every one additional year that a game was played, the annual average shot distance increases by 0.0134 feet, on average. This shows that the average distance of buzzer-beater shots has increased over time.
Interpretation of Intercept: In the year 0, the average distance of a buzzer-beater shot was -10.16 feet. This intercept is not meaningful, as the NBA did not exist in year 0, and a shot from negative feet would be made from behind the basket, which is against the rules of the NBA.
Factors that are associated with successful Buzzer-Beater Shots:
# A tibble: 4 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 9.60 1.20 8.01 5.79e-15
2 GmSc 0.291 0.0638 4.55 6.38e- 6
3 AssistYes 9.14 1.72 5.31 1.52e- 7
4 GmSc:AssistYes -0.201 0.0969 -2.07 3.86e- 2# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.107 0.102 9.74 24.4 6.10e-15 3 -2278. 4566. 4588.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Estimated Linear Model:
\[ \text{buzzer-beater shots} = 9.5958320 + 0.2905904 \times \text{Mean game score} \\ + 9.1403964 \times \text{AssistYes} - 0.2008358 \times (\text{Mean game score} \times \text{AssistYes}) \]
Interpretation of Intercept: 9.595832 represents the estimated probability of a successful buzzer-beater shot when all other variables (GmSc and AssistYes) are held constant at 0. In practical terms, this is the estimated probability of a successful shot when the Player Game Score (GmSc) is 0 and the shot is unassisted (AssistYes = 0).
Interpretation of slopes:
GmSc (0.2905904): This coefficient represents the change in the estimated probability of a successful shot for a one-unit increase in the Player Game Score (GmSc), when other variables are held constant. A higher positive coefficient of GmSc suggests that as the Player Game Score increases, the probability of a successful shot also tends to increase, indicating that higher-performing players may have a better chance of making a buzzer-beater shot.
AssistYes (9.1403964): This coefficient represents the estimated difference in the probability of a successful shot between an assisted (AssistYes = 1) and an unassisted (AssistYes = 0) buzzer-beater shot, when other variables are held constant. A positive coefficient of AssistYes suggests that assisted shots are associated with a higher probability of success compared to unassisted shots, indicating that passing or teamwork in the form of an assist may increase the likelihood of making a successful buzzer-beater shot.
Interaction term (GmSc:AssistYes) coefficient (-0.2008358): This coefficient represents the change in the association between Mean game score and the expected number of successful buzzer-beater shots depending on whether the shot is assisted or unassisted. A negative coefficient suggests that the relationship between Mean game score and the expected number of successful buzzer-beater shots may be weaker for assisted shots compared to unassisted shots, assuming all other factors remain constant. This could mean that players with higher game scores may be able to make successful buzzer-beater shots even without assists, while players with lower game scores may rely more on assists to increase their chances of success.
Game Score vs. Number of Game Winning Buzzer-Beater Shots made:
# A tibble: 1 × 1
r.squared
<dbl>
1 0.0302
Pearson's Chi-squared test
data: aggregated_results_chi_sq
X-squared = 6.9673, df = 7, p-value = 0.4323The R^2 value of the linear model predicting the number of game winning buzzer-beater shots made per player from each player’s average game score over the games where they have made such shots is equal to ~0.03. This would indicate that roughly 3% of the variability in number of buzzer-beater shots hit is explained by players’ average game score, which would indicate that this variable is not a good predictor of the number of such shots made by any measure. As a result, selecting a number of shots randomly will likely lead to more accurate predictions of a players’ buzzer-beater shot count than using this linear regression model would.
This conclusion is reinforced by conducting a chi-squared test of independence on the relationship between the number of game winning buzzer-beat shots hit and average game score. The hypotheses of this test were:
Null Hypothesis: Mean game score and number of game winning buzzer-beater shots made are not related.
Alternative Hypothesis: Mean game score and number of game winning buzzer-beater shots made are related; at least one mean game score for some number of game winning buzzer-beater shots made is significantly different than any other number of game winning buzzer-beater shots made.
With a p-value of 0.43 which is greater than alpha = 0.05, we fail to reject the null hypothesis. There does not appear to be a relationship between nean game score and the number of game winning buzzer-beater shots a player who has made at least one such shot has made.
Year vs. Average Distance from Basket of Buzzer-Beater Shot:
# A tibble: 1 × 1
r.squared
<dbl>
1 0.00169# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -10.2 74.7 -0.136 0.892
2 year 0.0134 0.0376 0.356 0.723# A tibble: 1 × 2
lower upper
<dbl> <dbl>
1 14.8 18.1# A tibble: 1 × 1
avg_dist
<dbl>
1 16.5
# A tibble: 1 × 1
p_value
<dbl>
1 0.952Null hypothesis: Annual average distance of buzzer-beater shots has not changed significantly over time.
Alternative hypothesis: Annual average distance of buzzer-beater shots has changed significantly over time.
The R^2 value for this model is very small at 0.00169. This means that only 0.169% of the variability in the average annual distance of game winning buzzer-beater shots made can be explained by the year a game took place. This makes sense since the findings show that the average annual distance of buzzer-beater, game-winning shots, has changed very little over time.
Furthermore, after conducting a two-tailed hypothesis test on average distance of these shots over time, we found the p-value to be 0.952, which is much higher than the alpha value of 0.05. Thus, we fail to reject the null hypothesis, meaning that the annual average distance of buzzer-beater shots has not changed significantly over time,
Factors that are associated with successful Buzzer-Beater Shots:
# A tibble: 1 × 1
r.squared
<dbl>
1 0.107[1] 5.785319e-15 6.383806e-06 1.518936e-07 3.864903e-02# A tibble: 4 × 2
term estimate
<chr> <dbl>
1 intercept 9.60
2 GmSc 0.291
3 AssistYes 9.14
4 GmSc:AssistYes -0.201# A tibble: 4,000 × 3
# Groups: replicate [1,000]
replicate term estimate
<int> <chr> <dbl>
1 1 intercept 17.6
2 1 GmSc -0.0476
3 1 AssistYes -0.677
4 1 GmSc:AssistYes 0.0796
5 2 intercept 18.3
6 2 GmSc -0.0521
7 2 AssistYes -2.14
8 2 GmSc:AssistYes 0.0939
9 3 intercept 18.5
10 3 GmSc -0.0701
# ℹ 3,990 more rows# A tibble: 4 × 3
term lower_ci upper_ci
<chr> <dbl> <dbl>
1 AssistYes -3.64 3.85
2 GmSc -0.133 0.137
3 GmSc:AssistYes -0.199 0.210
4 intercept 14.7 19.4 The R^2 value of the linear model predicting the distance of the buzzer-beater shots based on the game score, the number of assists, and the interaction between these two variables is 0.107. This indicates that 10.7% of the variability in the distance of the buzzer-beater shots is explained by the model.
Null Hypothesis: All predictor variables (assists, game score, and interaction between game score and assists) have no effect on the response variable (distance).
Alternative Hypothesis: At least one predictor variable has a significant effect on the response variable.
The p-values for the predictors in the model are very small (6.100504e-15 for GmSc, 9.1403964e-15 for Assist, and 0.03864903 for the interaction between GmSc and Assist), indicating that the model is highly significant. Therefore, we reject the null hypothesis and conclude that at least one predictor variable is significantly related to the distance of the buzzer-beater shots. The predictor variable that is most significantly related to the distance of the buzzer-beater shots is Assist, as it has the lowest p-value.
Game Score vs. Number of Game Winning Buzzer-Beater Shots made:
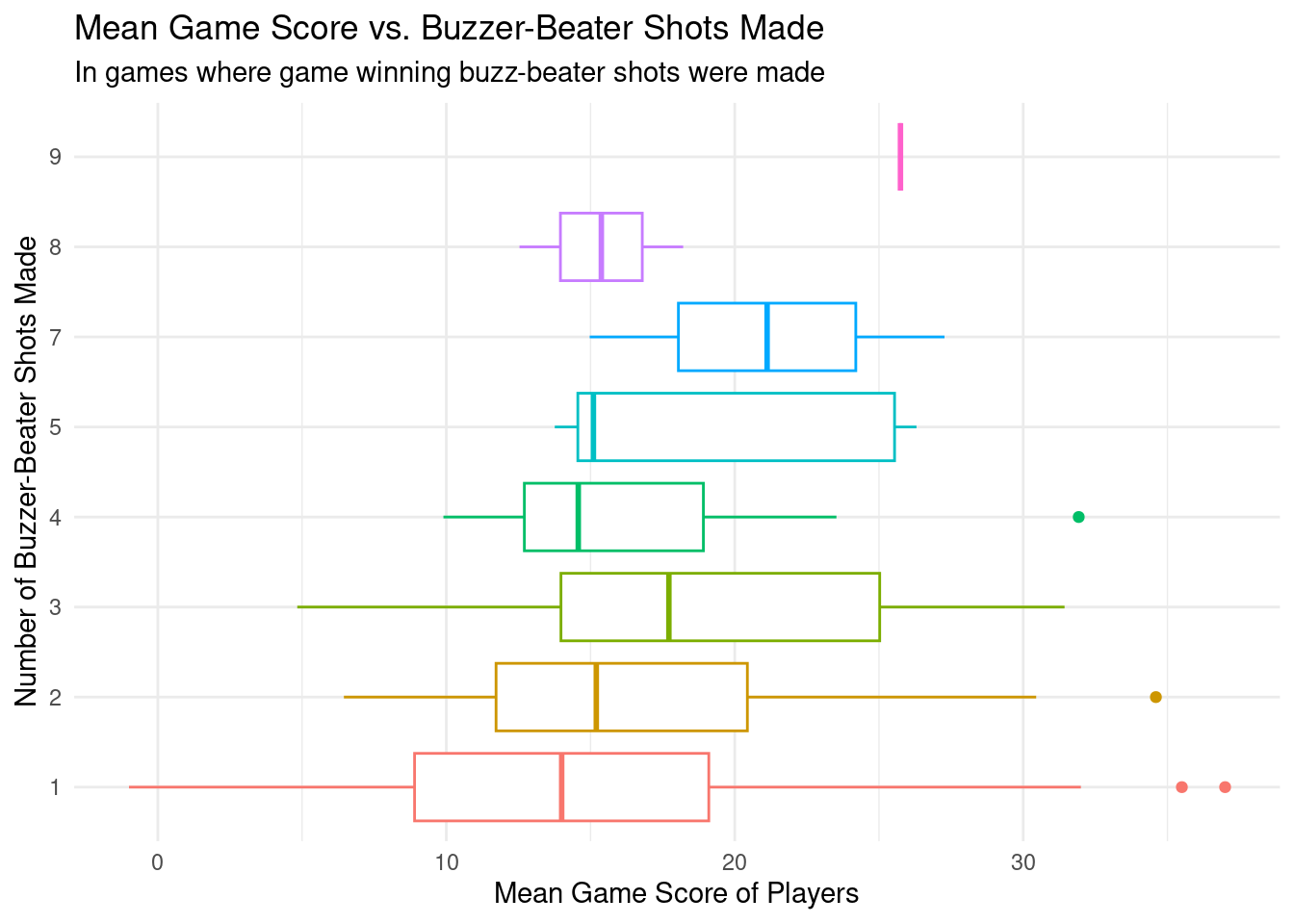
To answer the question of if, out of the pool of NBA players who have made game winning buzzer-beater shots, players who performed better on average in games where they scored a game winning buzzer-beater shot were those who made the most buzzer-beater shots as we originally hypothesized, we first visualized the relationship between average game score and number of such shots hit for each player as a boxplot. This plot alone did not reveal any significant relationship between these two variable. While it is true that those who only scored 1 game winning buzzer-beater had the lowest median game score at ~14, and the player who scored the most of these shots at 9 had the highest median game score of ~26, there is no clear uniform trend in the data that suggests a correlation between these variables. For example, those players who hit 4 or 5 buzzer-beater shots in their careers had lower median game scores than those who hit 2 or 3.
Failing to identify a relationship from this boxplot, we then created a linear regression model to be able to predict the number of buzzer-beater shots a player could be expected to make based off of their average gamescore. In our evaluation of the model’s significance, we calculated the R^2 value to be equal to ~0.03 and concluded that this model is not useful, accounting for only 3% of the variability in number of game winning buzzer-beater shots hit as determined by average game score, or, in other words, how well those players performed on average in games where they hit a game-winning buzzer-beater shot. To further test if there is a relationship between these variables, we conducted a chi-squared test of independence between them. This test, with a high p-value of 0.43, failed to detect any relationship between the number of game winning buzzer-beater shots made and average game score of all players who have hit some number of these shots. This further reaffirms that the two variables are independent. From these results, we conclude that game performance is very likely not representative of a players’ ability to make a game winning buzzer-beater shot.
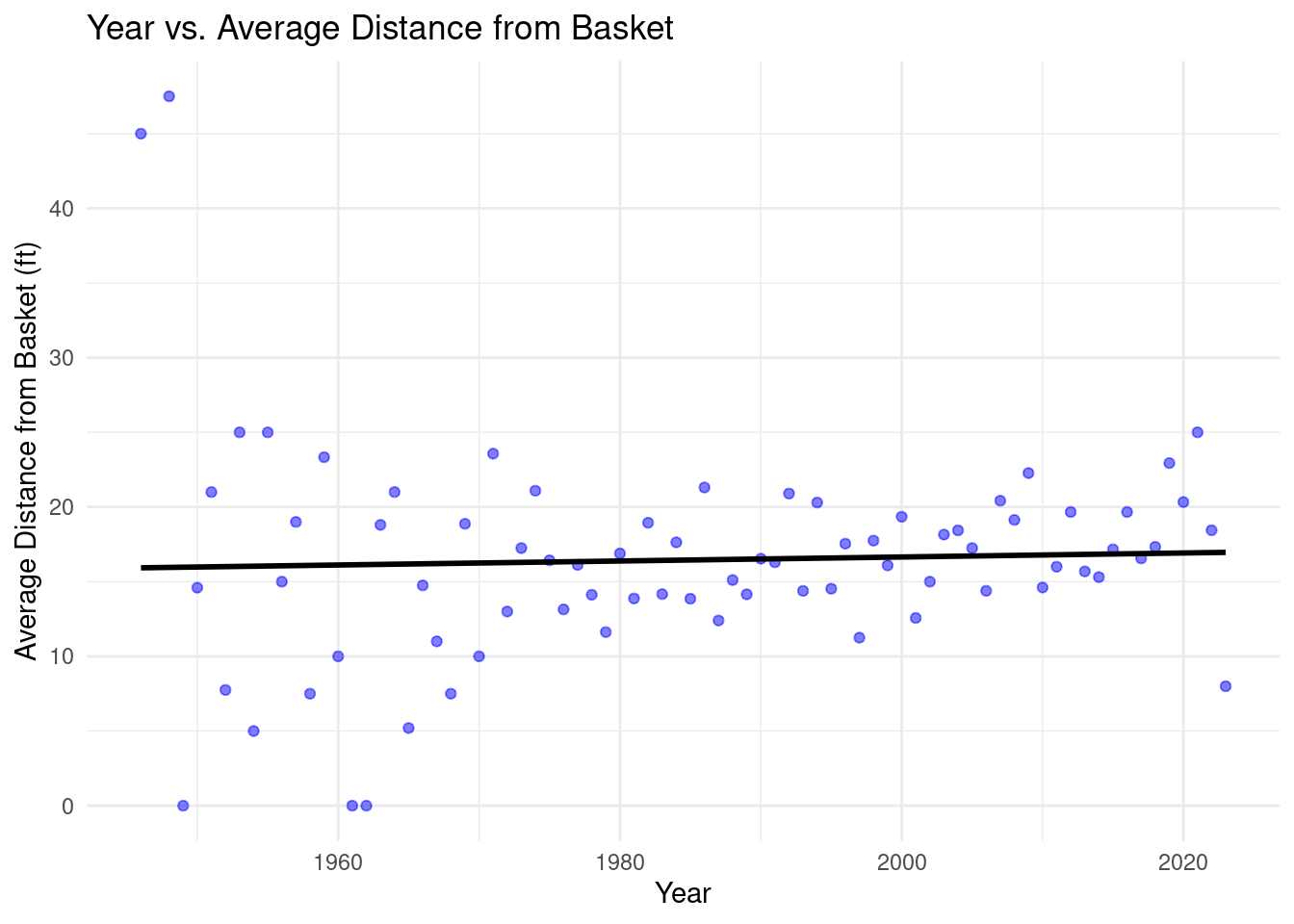
Year vs. Average Distance from Basket of Buzzer-Beater Shot:
We had initially hypothesized that the average distance from the basket of a buzzer-beater shot has increased over time as more adept players have played professional basketball with better coaching, nutrition plans, etc. Nonetheless, this proved to be untrue as the model shows that the distance has only increased very slightly by, according to the model, only about 0.0134 feet per year, on average. As shown on the graph, the average distance from the basket has not been 0ft since 1962, showing that there has been an increase over time. However, this change did not appear to be statistically significant.
The R^2 value of the model is very small at 0.00169, indicating that the model does not offer a lot in terms of explaining the variability in average shot distance. The lower bound of a 95% confidence interval of the average distance is 14.79 feet and the upper bound is 18.12 feet, making the average range very small, also indicating that the average distance has not changed too much over time. The p-value is also very high at 0.952, again showing that there has not been much change. Year and average distance thus do not appear to be correlated.
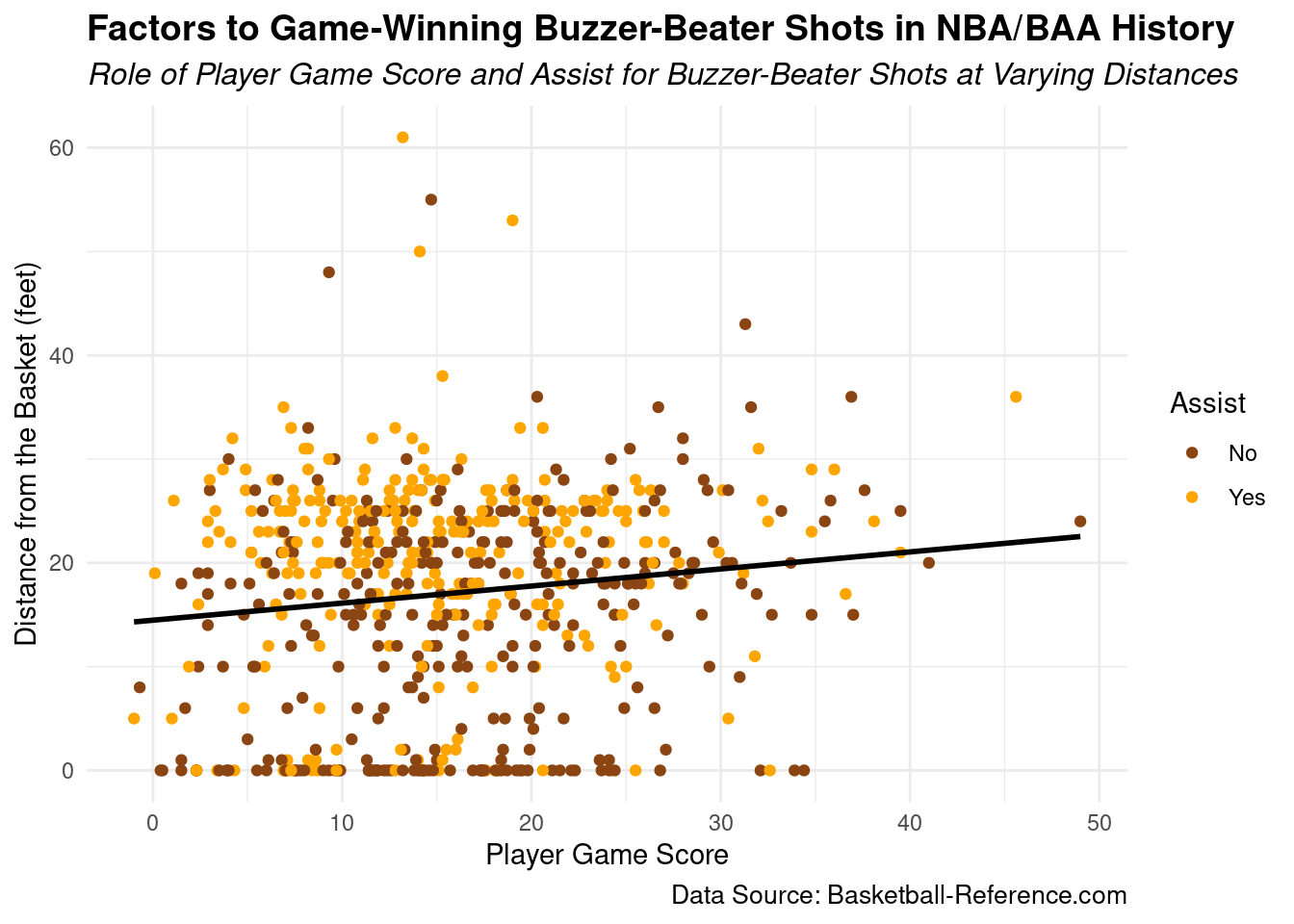
Factors that are associated with successful Buzzer-Beater Shots:
We then tested our hypothesis that game score combined with whether or not the shot was assisted contributed to the success of a game winning buzzer-beater shot. In our analysis, we found that these variables were significant predictors of the distance of buzzer-beater shots, with assists having the strongest relationship. The model showed that players were more likely to make successful buzzer-beater shots when they were assisted, indicating that teamwork and passing play a significant role in the success of buzzer-beaters. Additionally, higher-performing players, as indicated by their game score, were more likely to make successful buzzer-beater shots. However, our model only explained 10.7% of the variability in the distance of the shots, suggesting that other factors, such as the shooter’s skill level and defense’s positioning, may also be significant factors in the success of buzzer-beater shots.
We are confident in this conclusion because our analysis employed a rigorous statistical model that controlled for confounding variables and examined the significance of each predictor variable. The small p-values for the predictor variables in our model indicate that the model is highly significant, and we were able to reject the null hypothesis that the predictor variables had no effect on the response variable. These findings suggest that passing and teamwork are essential for successful buzzer-beater shots, and higher-performing players may have an advantage in making these shots.
General Conclusions and Future Work:
In the context of real-life basketball games, our analysis highlights the importance of teamwork and individual performance in determining the success of buzzer-beater shots. Coaches and players may want to consider these findings when developing game strategies and identifying players to take crucial last-second shots. Additionally, our results suggest that further research could investigate the impact of other factors, such as shooter’s skill level and defense’s positioning, on the success of buzzer-beater shots.
However, while these quantifiable factors may be indicators of higher rates of success, it is also very likely that the ability to consistently make game winning buzzer-beater shots comes down to, as far as the data is concerned, simple randomness. The real world is much more complicated than regression models, and major performance indicators also include non-quantifiable factors, such as a players’ ability to perform well under intense pressure. These qualities are difficult to measure, and will very player-by-player and game-to-game. This suggests that, while player stats may be useful, it is also up to the coaches to assess their players within the context of each game when picking a strategy to employ should the opportunity arise to attempt one of these shots.
In the future, further analyses could be conducted on more of the variables in the dataset to determine other possible correlations. Furthermore, similar analyses could be applied to other sports (e.g. last-second touchdown attempts in Football) to attempt to get an insight into the factors that make scoring synonymous goals, shots, runs, etc… more likely. Based on our results in this study, it is likely that similar conclusions would be drawn from similar studies on other sports, the most significant of which is that players are more than their statistics.
The major limitation of this dataset is that it does not include games with unsuccessful buzzer-beater attempts. This makes it difficult to analyze shot success rates for a player, team, game, or year and to draw conclusions from the dataset that apply to the NBA in general since the dataset is not representative of every NBA game in history.
Additionally, the dataset does not contain some of the information for games before 1979, specifically related to 3-point field goals. The records of games before this year were either not as thorough or not obtainable, and thus some of the data available for games during and after 1979 is not available anymore to be collected, at least not that the creators of the dataset could find. This results in many null values for some of the columns in these earlier years.
Both of these limitations were and should be kept in mind when working with this data to ensure it is not used to make erroneous conclusions outside of the scope of where it applies, which is specifically NBA games that have been decided by a successful buzzer-beater shot.
Stack Overflow was referenced to create a new string for the “year” variable in analysis #2.
The dataset employed in this study comes from Basketball Reference.com (https://www.basketball-reference.com/). We are thankful to the creators of this dataset for putting it together and making it freely available to the public.
Finally, we would like to thank Benjamin Soltoff, without whose instruction this report would not have been made.