Introduction and Motivation
Motivation: As we came from all sorts of different background, we realized there are huge difference in culture and economic system. With our data set and analysis, we want to further explore what makes up some of the wealthiest people in the world and how it affect their decisions.
Goal: We want to discover the relationship between a person’s education level on their net worth and whether their net worth affect how much children they have.
The two primary topics:
- The influence of education on wealth of individuals
- The influence of wealth on family size
Introduce the data
Billionaires data set was used, to measure the different demographic charachteristics and their affect on the wealth of each individual. We were interested in studying wealth and it’s influence on society.
We have three different sections for our analysis.
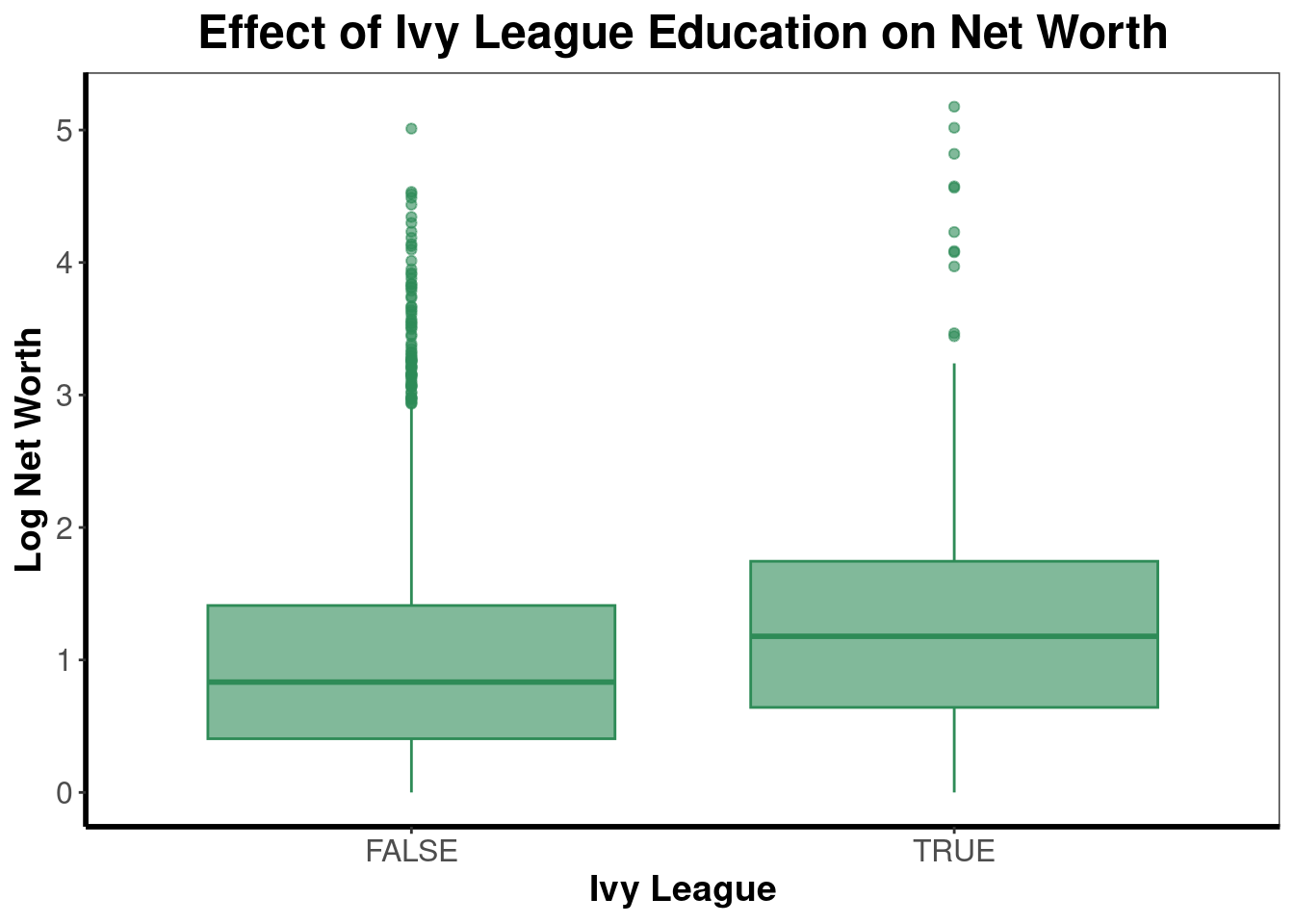
- Ivy League vs Net worth
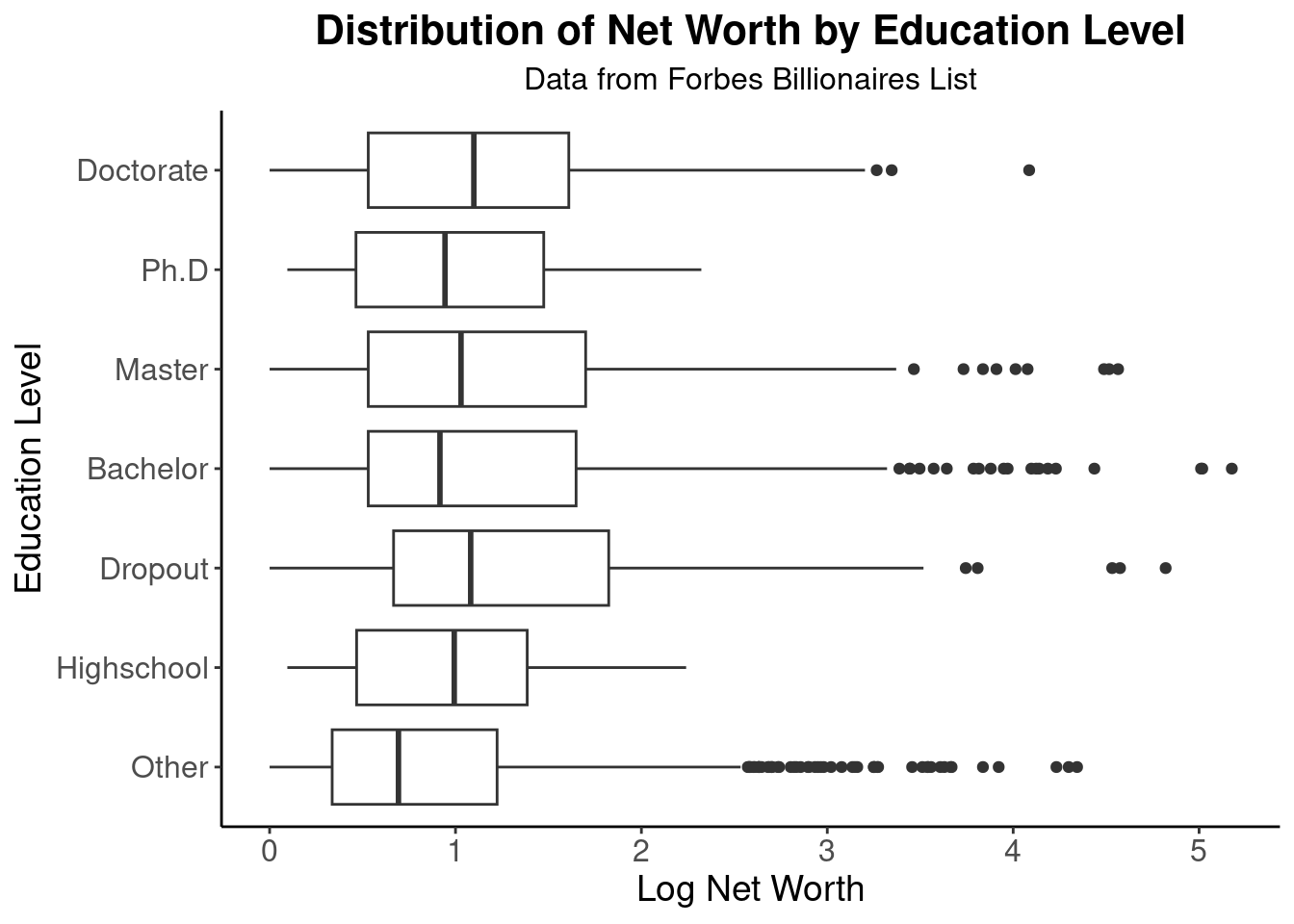
- Education level vs Net worth
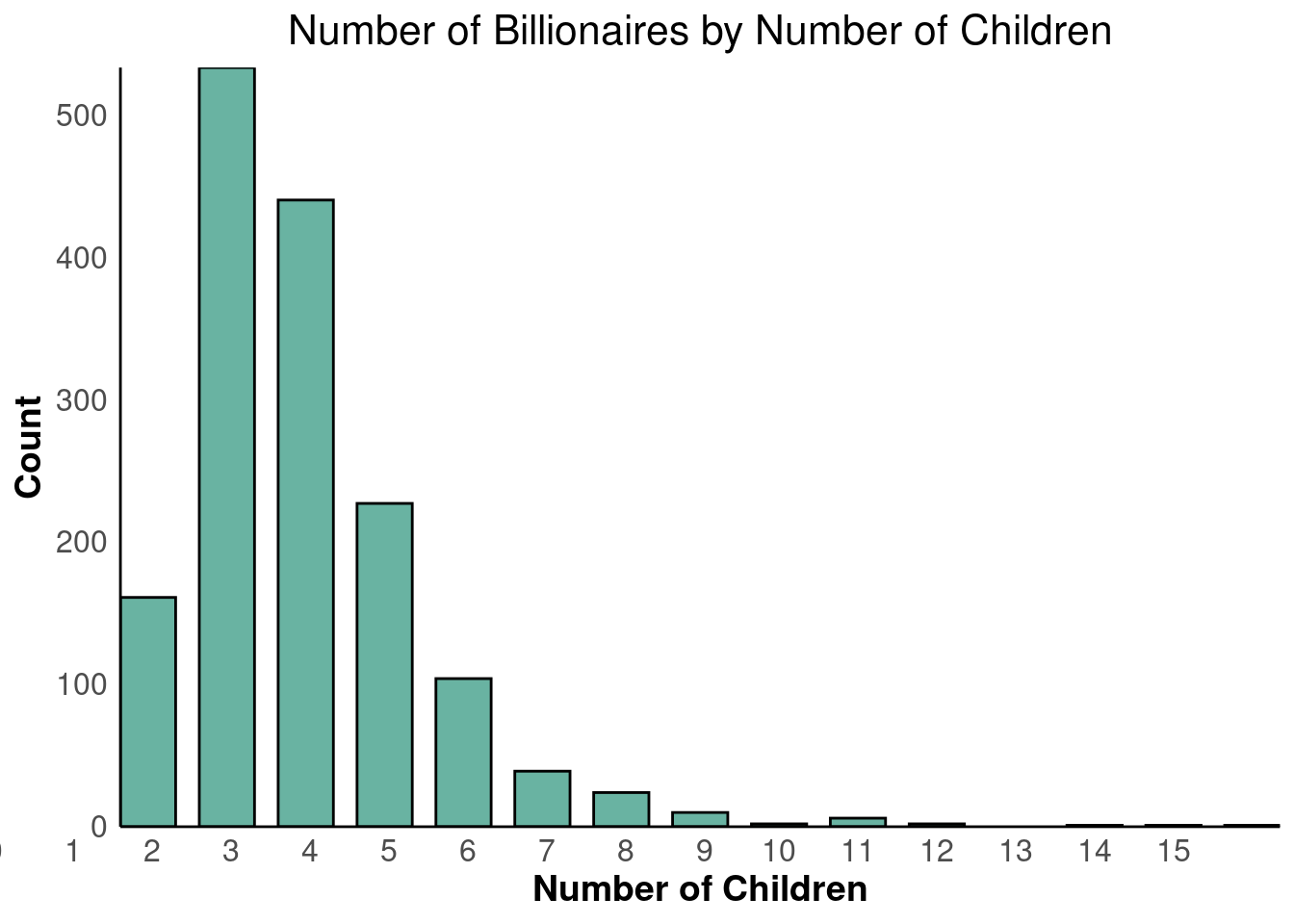
- Number of Children vs Net worth
# A tibble: 2 × 5
ivy_league mean_net_worth median_net_worth min_net_worth max_net_worth
<lgl> <dbl> <dbl> <dbl> <dbl>
1 FALSE 4.42 2.3 1 150
2 TRUE 8.33 3.25 1 177
# A tibble: 1 × 4
mean_children mean_networth min_networth max_networth
<dbl> <dbl> <dbl> <dbl>
1 2.98 4.75 1 177
Inference Analysis 1
First analysis: Education vs Net worth
\[
\newcommand{\indep}{\perp \!\!\! \perp}
\newcommand{\nindep}{\not\!\perp\!\!\!\perp}
H_0: net~worth \indep education\\
H_1: net~worth \nindep education\
\]
# A tibble: 3 × 2
term estimate
<chr> <dbl>
1 intercept 16.4
2 years_education -0.601
3 ivy_leagueFALSE -3.24
# A tibble: 3 × 2
term p_value
<chr> <dbl>
1 intercept 0.918
2 ivy_leagueFALSE 0.93
3 years_education 0.918
Our null hypothesis is that there is no relation between a person’s education level and their total net worth.
Our alternative hypothesis is that there is a relation between a person’s education level and their total net worth.
For our first analysis, we found out that there is no relationship between a person’s education level and their total net worth. We determined this since the p value for this was 0.919 which was extremely high and much greater than 0.05. As a result, we reject the alternative hypothesis.
Inference Analysis 2
Second analysis: Number of Children vs Net worth
\[
\newcommand{\indep}{\perp \!\!\! \perp}
\newcommand{\nindep}{\not\!\perp\!\!\!\perp}
H_0: number~of~children \indep net~worth\\
H_1: number~of~children \nindep net~worth
\]
# A tibble: 9 × 2
term estimate
<chr> <dbl>
1 intercept 2.86
2 net_worth 0.00587
3 statusEngaged -0.871
4 statusIn Relationship 0.603
5 statusMarried 0.0635
6 statusSeparated 0.237
7 statusSingle 0.187
8 statusWidowed 0.429
9 statusWidowed, Remarried 0.590
# A tibble: 9 × 2
term p_value
<chr> <dbl>
1 intercept 0.968
2 net_worth 1
3 statusEngaged 0.979
4 statusIn Relationship 0.978
5 statusMarried 0.984
6 statusSeparated 0.922
7 statusSingle 0.9
8 statusWidowed 0.958
9 statusWidowed, Remarried 0.881
Our null hypothesis is that there is no relation between a person’s net worth and how much children they have.
Our alternative hypothesis is that there is a relation between a person’s net worth and how much children they have.
For our second analysis, we have determined that there is also no relationship between a person’s education. We came to this conclusion since the p value for this was 0.968 which is extremely high. As a result, we can once again reject the alternative hypothesis.
Conclusions + Future Work
We came to the conclusion that the net worth of a person is not affect by a person’s education level nor do they affect a person’s number of children.
This shows that becoming a billionaire does not necessarily require formal education, but other external factors such as creativity and hard work might be even more important.
In our future work, we believe we can have more accurate and concise data such as how dropout does not specify whether a person dropped out from high school, bachelor, or doctorate. This data also might not include every single billionaire since there might be people who does not make their net worth public which can affect the data greatly.