The goal of this lab is to implement a Bayes filter in a simulated environment before implementing it on the robot. The Bayes filter will predict the location of the robot data from the mapping function from lab 9. The first step to do this was to create a function that computes the motion between two points. The odometry model was chosen for it's strength in localization of the robot, and it's inability to predict the robot's next move is not needed. The function was implemented as below.

The function will calculate the control vector (size three array for δ_{rot_1}, δ_trans, and δ_{rot_2}) for each value in current_pose given each prev_pose. The odometry model then found the likelihood of having the calculated result given control vector u, using the gaussian function with standard deviations determined from the deviation of sensor data. The odometry model was implemented as below.

This model was then used in the prediction step to calculate the probability matrix of each potential current position given the previous position and control vector. It then takes a weighted sum of those probability matrices, with the weights coming from the belief matrix indicating the likelihood of being at that position. The implementation is shown below.

This step reduces the uncertainty in the robot's position. Given an observation (18 distance sensor measurements taken at 20° steps around the robot's position) the sensor model will calculate the probability of the robot being at each position on the map. Below is the implementation of the model.

Then each of these probabilities are weighted by the previous belief of the robot.

The robot then finds it's position by finding the most likely position. The robot was run through the tracjectory in the given notebook and its believed location was plotted after it moved to a new position and performed an observation on it. Below is a video showing a great performance of the algorithm at work. The blue data is the belief of the robot at different points in time, and the green data is the true position.

The results of the bayes filter on this run are tabulated below./

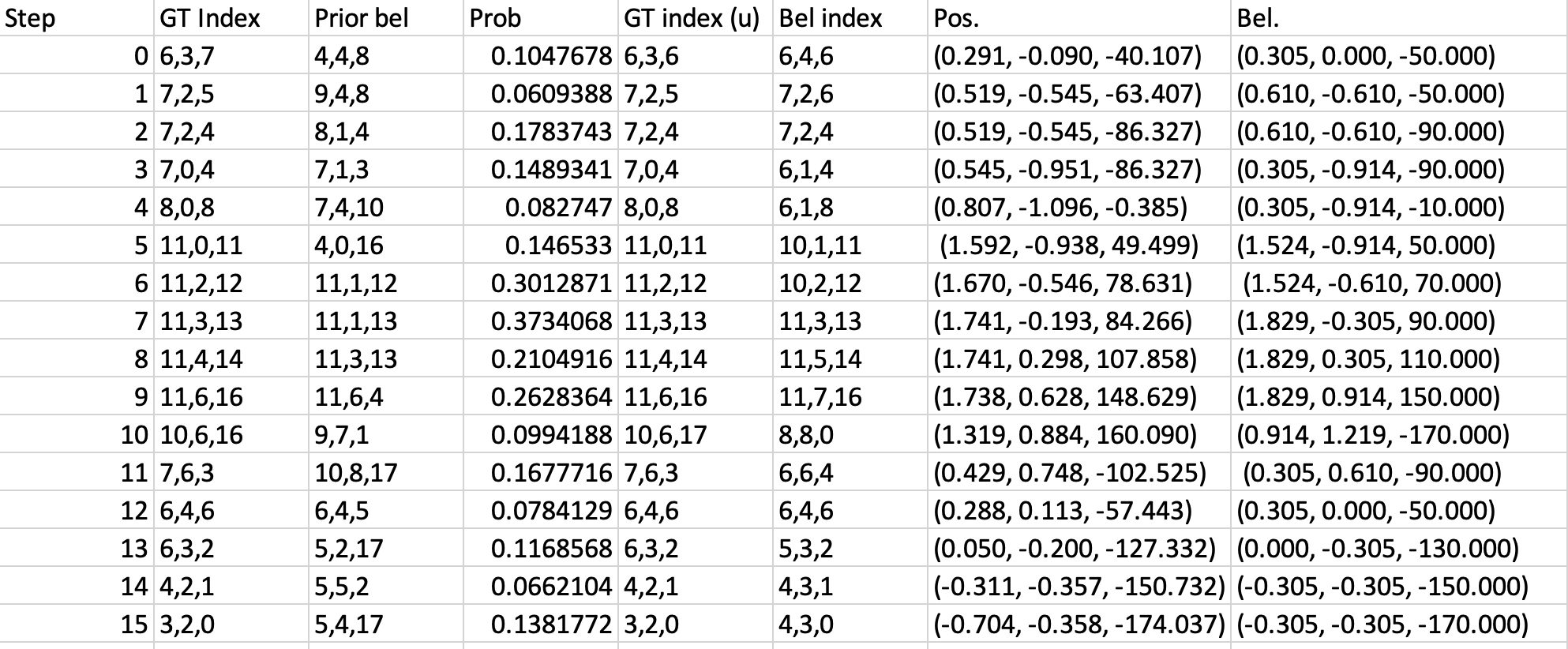
From the data it seems that the model is great at finding cells with angles closest to the observed point, at the cost of being more uncertain in terms of position. This may have affected the accuracy of beliefs that were similar in angle but different in position.