Ryan's ECE 4960 Site
Lab 6
This lab was dedicated to implementing PID control to perform a specific task. For my task, I chose to stop in front of a wall at exactly 300 mm.
Bluetooth Prelab
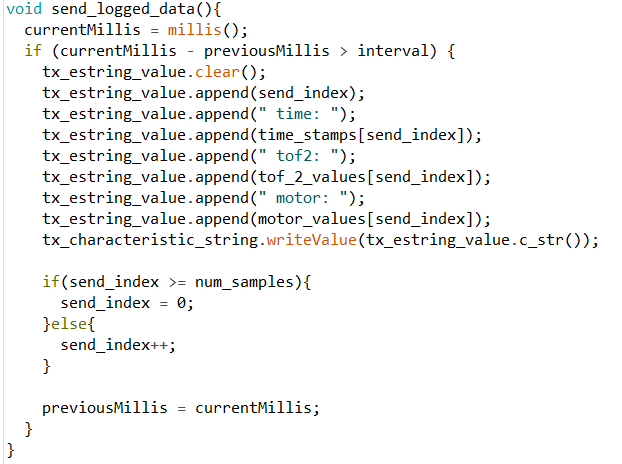
For this lab, it is essential to get data about the sensors and motor outputs to debug our PID
code and parameters, but since the robot is moving, it cannot be tethered to the computer. To
solve, this I implemented a system that uses the Aretmis' Bluetooth Low Energy (BLE) to send
information back. Since each Bluetooth transmission takes a non-insignificant amount of time
and since the robot requires very fast sensor sampling for PID to work effectively, I decided not to
send the data while the robot was performing its task. Instead, all the data is logged into arrays
while the robot is running its PID loop for about 15 seconds. When the robot is finished at the
end of the 15 seconds, it will send the data to a computer running a Python script.
Here is how I implemented the data storing and transmission on the Artemis side:

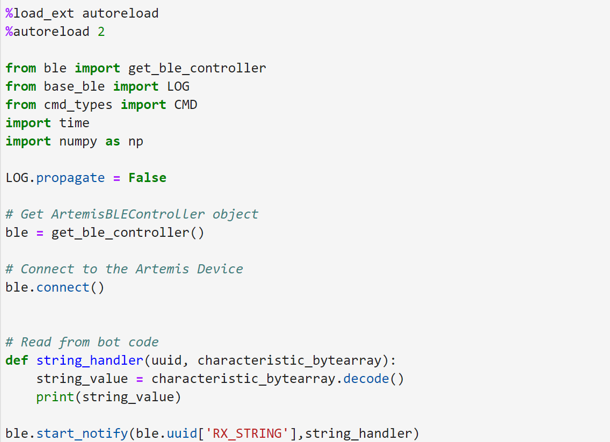
Here is how I implemented the data receiving on the computer Python side along with its output:

The PID Loop
The task I chose to accomplish using PID was to stop my robot in front of a wall at exactly 300mm. To do this, I used a Time of Flight sensor attached to the front of my robot to collect my necessary data. I then subtracted my target distance of 300mm from this current measured value to get the error that I fed into my PID loop. After much testing (described below), I found that I just needed a proportional and integral term for my loop, so I made a PI controller. Here is how I implemented this PI controller:

Testing and PID Tuning
To guide how I tuned my PI controller, I decided to use Heuristic #2 described in lecture. In this
heuristic, you set both KP (proportional gain) and KI (integral gain) to 0. To tune KP, you increase KP
until it oscillates, then decrease it by a factor of 2 to 4. After that, you tune KI by increasing it until
a loss of stability.
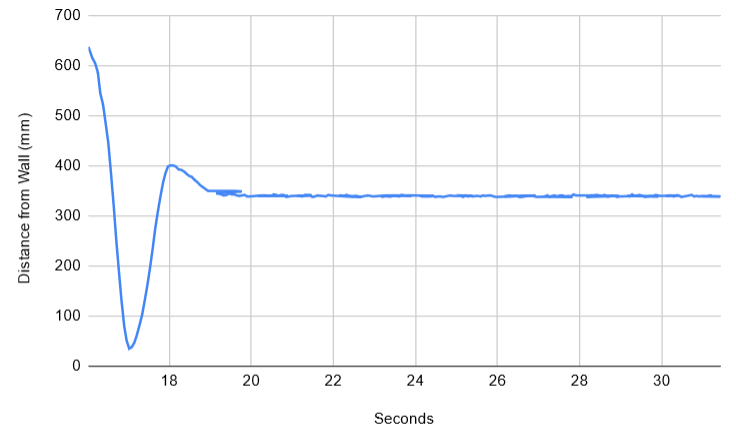
Based on the steps described above, I first implemented the proportional term (shown above). To get my KP, I increased my KP until it started oscillated, which I found to be 0.5.
Below is a graph and video of this run with the KP set to 0.5:
I then decreased the KP term (0.5) by a factor of 2 according to the heuristic to get 0.25. Below is a graph and video of this run with the KP set to 0.25:
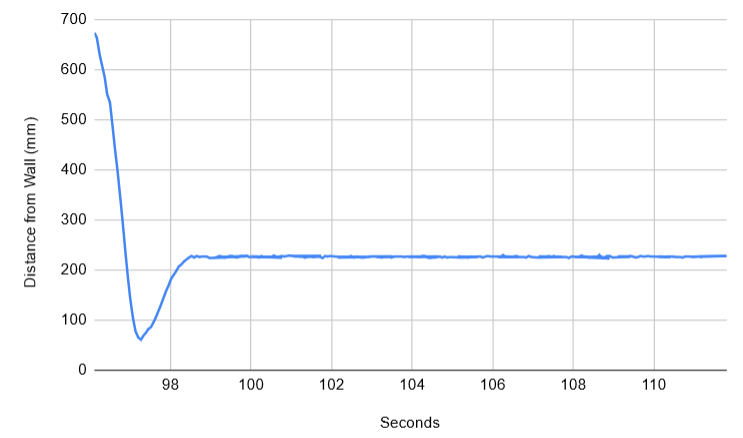
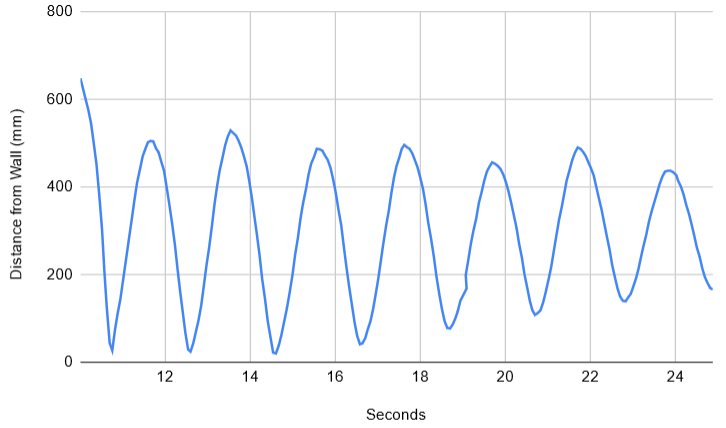
I found that with just the proportional term, the robot ended up stopping at around 225mm instead of the target 300mm, which led me to next implement the integral term. While implementing this, I determined that code to handle integral windup was necessary to keep the robot from going too fast and ramming into the wall the farther away it is from the wall. After I implemented this code (shown above), I then tried tuning the KI constant by following the heuristic by starting small and increasing until a loss of stability. I started with 0.1 which I thought was "small", but that turned out to be way too big and caused significant oscillations which can be seen in both the graph and video below:
I then reduced the KI term to 0.02, which ended up working very well to bring it to the exact 300mm target distance. Below is a graph and video of this run with the KI set to 0.02 (and the KP still at 0.25):
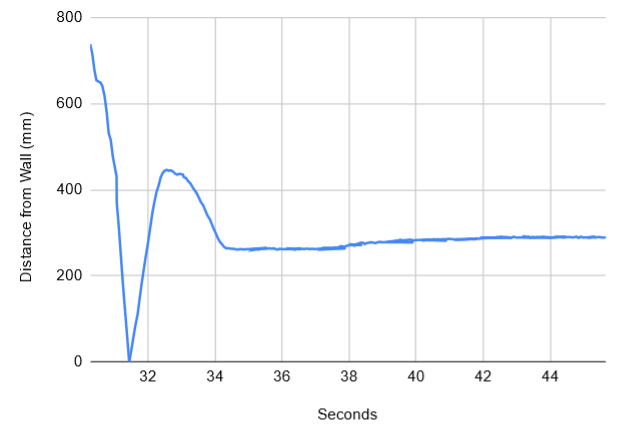
However, as can be seen in the video and graph, the addition of the integral term also gave the robot extra speed. This caused it to ram into the wall and also caused more oscillations than when there was just a proportional term. To resolve this, I decided to implement a somewhat hacky solution of adding in a sudden brake as soon as it crosses the target point to absorb some of the extra momentum. This ended up working extremely well and I was able to get it to hit the 300mm target distance with minimal oscillation as can be seen in the below graph and video:
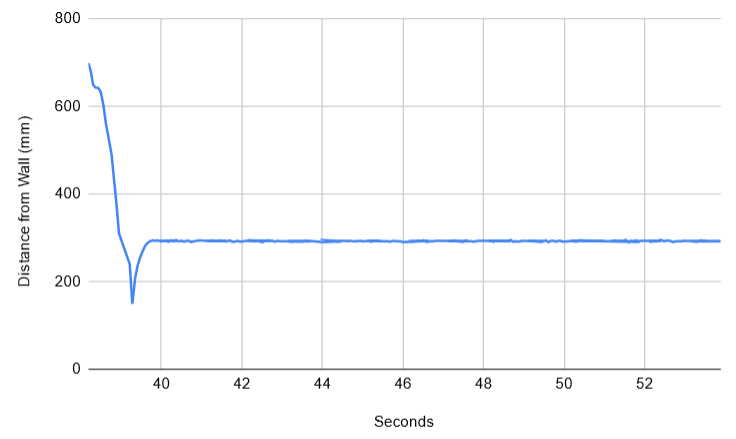
Below are two additional runs with the same exact settings to confirm that it can work reliably and repeatably:
Based on the data collected from the above run, I found that the maximum linear speed was about 1083 mm/s, which is fairly fast for such a small robot. However, I believe that it can run faster if it wasn't limited by its slow sampling rate. Although I've taken steps like avoiding delays and not sending BLE data during the PID loop, each loop iteration still takes around 0.06 seconds, which limits the sampling frequency to about 16 samples per second. Hopefully, the speed can be improved by implementing a Kalman Filter in Lab 7.